Gedetailleerde analyse van RC Series Circuit
2024-05-08
20524
Het RC -seriecircuit, bestaande uit een weerstand en een condensator, dient als een fundamentele component in zowel basis- als geavanceerde elektronische systeemontwerpen.Het helpt bij het begrijpen van belangrijke principes zoals frequentierespons, faseverschuiving en signaalfiltering, die een belangrijke rol spelen bij circuitontwerp en signaalverwerking.Deze verkenning omvat theoretische basisprincipes en strekt zich uit tot praktische toepassingen door middel van experimenten en simulaties.Door het circuit fysiek samen te stellen of digitaal te modelleren, kunnen leerlingen het laadproces visueel begrijpen en de effecten van component V ariat -ionen, waardoor complexe concepten toegankelijker en memorabeler worden.
Catalogus
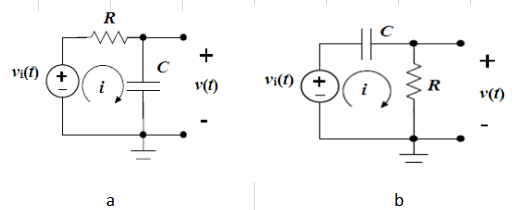
Figuur 1: Verschillende uitgangsspanningen van RC -circuits
Inleiding tot RC Circuit
Een RC-circuit, kort voor weerstandscapaciteitscircuit, is van fundamenteel belang in elektronica voor het manipuleren van signalen door weerstanden en condensatoren.Deze circuits staan vooral bekend om hun vermogen om fasen te verschuiven en signalen te filteren, met behulp van eenvoudige arrangementen van deze componenten.Een eenvoudig RC-circuit, vaak aangeduid als een RC-circuit van de eerste orde, bevat meestal slechts één weerstand en één condensator.
In een typische opstelling wordt de ingangsspanning toegepast op de serie -opstelling van een weerstand en een condensator.De output kan worden getrokken over de weerstand of de condensator, elk met verschillende reacties op signaalfrequenties vanwege de unieke kenmerken van de condensator.Met deze veelzijdigheid kunnen RC -circuits een verscheidenheid aan rollen uitvoeren in elektronische apparaten, zoals koppelings- en filteringssignalen of zelfs het converteren van golfvormen wanneer ze worden onderworpen aan een stapspanning.
Het RC-circuit kan op verschillende manieren worden geconfigureerd-serie, parallel of een combinatie van beide, bekend als serie-parallel.Elke configuratie beïnvloedt signaalfrequenties anders: serieverbindingen verzwakken de neiging om lage frequenties te verzwakken, terwijl parallelle verbindingen worden gebruikt om hogere frequenties te dempen.Dit verschil is voornamelijk te wijten aan de manier waarop weerstanden en condensatoren interageren met het circuit;Weerstanden verzetten zich rechtstreeks tegen de stroom, terwijl condensatoren deze opslaan en vrijgeven, wat beïnvloedt hoe het circuit reageert op verschillende frequenties.
In tegenstelling tot circuits met inductoren, zoals LC -circuits, kunnen eenvoudige RC -circuits niet resoneren omdat weerstanden geen energie opslaan.Dit kenmerk heeft duidelijk invloed op hoe RC -circuits worden gebruikt, gericht op hun vermogen om te filteren in plaats van energieopslag of resonantie.Elke configuratie dient een specifiek doel, waardoor RC -circuits veelzijdige tools worden in zowel theoretische studie als praktische toepassing in elektronisch ontwerp.
RC -serie circuit
Een RC -serie circuit, in wezen samengesteld uit een weerstand (R) en een condensator (C) in serie, werkt volgens een eenvoudig principe.Wanneer de schakelaar van het circuit is gesloten, begint de condensator van de toegepaste spanning op te laden (V), het initiëren van een stroomstroom door het circuit.Naarmate de condensator oplaadt, neemt de stroom geleidelijk toe totdat de condensator zijn capaciteit bereikt, op welk punt het stopt met het accepteren van lading, en de stroom stabiliseert op zijn maximale waarde, berekend als 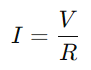 .
.
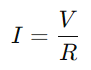 .
.Het laadproces van de condensator kan wiskundig worden beschreven door de vergelijking 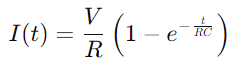 , waar ik de stroom is, V is de spanning, R is de weerstand, C is de capaciteit, T is tijd, en e is de basis van de natuurlijke logaritme.Deze formule weerspiegelt hoe de stroom in de loop van de tijd verandert als de condensator, waarbij het product van de weerstands- en capaciteitswaarden (RC) de tijdconstante van het circuit definieert, indicatief voor de snelheid waarmee de condensator laadt.
, waar ik de stroom is, V is de spanning, R is de weerstand, C is de capaciteit, T is tijd, en e is de basis van de natuurlijke logaritme.Deze formule weerspiegelt hoe de stroom in de loop van de tijd verandert als de condensator, waarbij het product van de weerstands- en capaciteitswaarden (RC) de tijdconstante van het circuit definieert, indicatief voor de snelheid waarmee de condensator laadt.
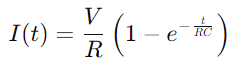 , waar ik de stroom is, V is de spanning, R is de weerstand, C is de capaciteit, T is tijd, en e is de basis van de natuurlijke logaritme.Deze formule weerspiegelt hoe de stroom in de loop van de tijd verandert als de condensator, waarbij het product van de weerstands- en capaciteitswaarden (RC) de tijdconstante van het circuit definieert, indicatief voor de snelheid waarmee de condensator laadt.
, waar ik de stroom is, V is de spanning, R is de weerstand, C is de capaciteit, T is tijd, en e is de basis van de natuurlijke logaritme.Deze formule weerspiegelt hoe de stroom in de loop van de tijd verandert als de condensator, waarbij het product van de weerstands- en capaciteitswaarden (RC) de tijdconstante van het circuit definieert, indicatief voor de snelheid waarmee de condensator laadt.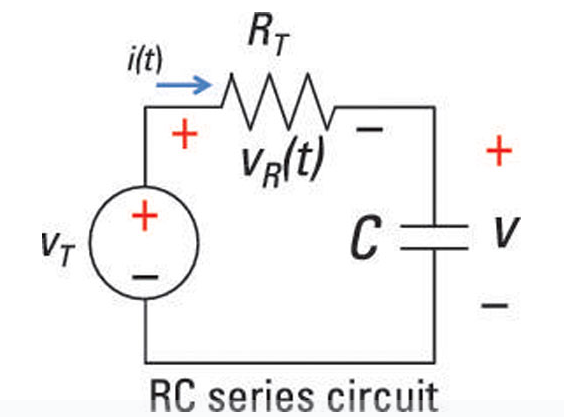
Figuur 2: RC -serie circuit
Ontladen treedt op wanneer de schakelaar wordt geopend, waardoor het proces wordt omgekeerd: de opgeslagen energie in de condensator wordt vrijgegeven, waardoor de stroom in de tegenovergestelde richting stroomt totdat de condensator is afgevoerd.Deze laad- en ontlaadcyclus is cruciaal in toepassingen zoals signaalconversie, filtering en timingcircuits vanwege de voorspelbare manier waarop de stroom- en spanningsverandering.
Figuur 3: RC -serie kortsluiting
Het gedrag van het RC -seriecircuit varieert ook met frequentie.Bij lage frequenties werkt de condensator meer als een open circuit, dat de stroomstroom sterk belemmert.Naarmate de frequentie toeneemt, neemt de capacitieve reactantie af, waardoor het voor de stroom gemakkelijker wordt om door te gaan.Met deze verandering in impedantie met frequentie kan het RC -seriecircuit als een filter fungeren, waardoor selectief frequenties onder een bepaalde drempel worden verzwakt (draaiende frequentie 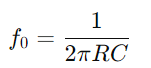 ).
).
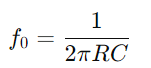 ).
).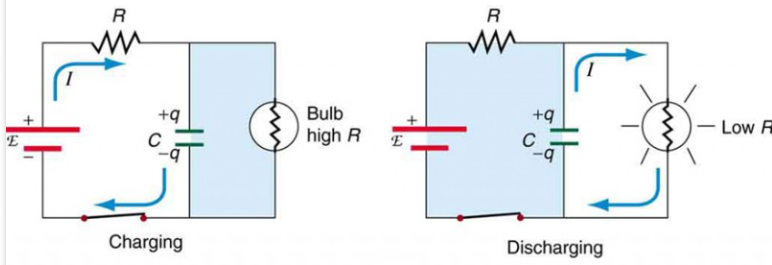
Figuur 4: Opladen en ontladen van RC -seriecircuits
Naast steady-state bewerkingen worden RC-circuits ook bestudeerd op hun tijdelijke reacties wanneer ze worden onderworpen aan plotselinge spanningsveranderingen, zoals wanneer een DC-voeding wordt ingeschakeld of uitgeschakeld.Dit scenario wordt een voorbijgaand proces genoemd, waarbij het circuit van de ene stabiele toestand naar de andere overgaat.De dynamiek van dit proces hangt aanzienlijk af van de RC -tijdconstante, die regeert hoe snel het circuit reageert op veranderingen.
Uiteindelijk dienen RC -seriecircuits meerdere functies in zowel DC- als AC -toepassingen, waarbij taken worden behandeld, variërend van het uitstellen van signalen tot het integreren of koppelen van verschillende circuitelementen.Deze veelzijdigheid komt voort uit de unieke interacties tussen de weerstand en de condensator, die samen de algehele respons van het circuit op veranderingen in spanning en frequentie bepalen.
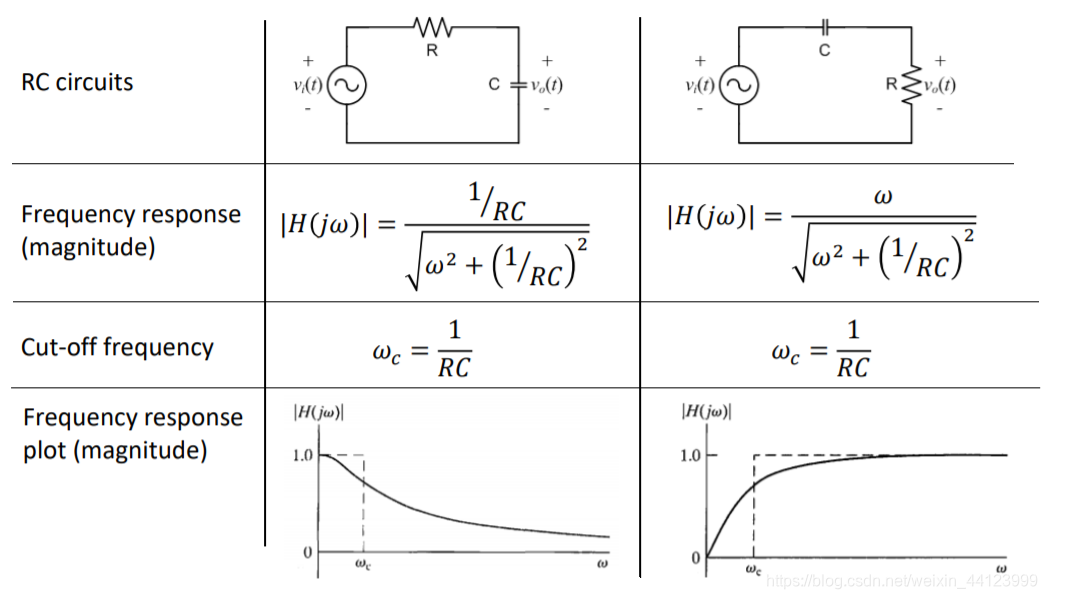
Figuur 5: RC -serie circuitdiagram en frequentieformule
In een Circuit van een RC -serie, het samenspel tussen de weerstand (R) en de condensator (C) invloeden zowel stroom- als spanningsverdeling.De primaire rol van de weerstand is het reguleren van de huidige stroom.Deze relatie wordt gekwantificeerd door de wet van Ohm, die stelt 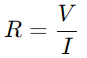 , waar V is spanning en I is actueel.In wezen fungeert de weerstand als een knelpunt en regelt hoeveel elektriciteit op elk willekeurig moment kan passeren.
, waar V is spanning en I is actueel.In wezen fungeert de weerstand als een knelpunt en regelt hoeveel elektriciteit op elk willekeurig moment kan passeren.
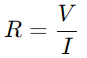 , waar V is spanning en I is actueel.In wezen fungeert de weerstand als een knelpunt en regelt hoeveel elektriciteit op elk willekeurig moment kan passeren.
, waar V is spanning en I is actueel.In wezen fungeert de weerstand als een knelpunt en regelt hoeveel elektriciteit op elk willekeurig moment kan passeren.De functie van de condensator is iets ingewikkelder omdat deze tijdelijk elektrische energie opslaat en vervolgens terug in het circuit wordt vrijgeeft.De spanning over de condensator (VC) correleert met zijn opgeslagen lading (Q) en wordt berekend met behulp van de formule  .Deze relatie benadrukt de capaciteit van de condensator om lading vast te houden, wat direct invloed heeft op de spanning die het vertoont.Tijdens de werking is de dynamiek van het opladen en ontladen van de condensator van vitaal belang voor het begrijpen van RC -circuits.De tijdconstante (τ), gedefinieerd als
.Deze relatie benadrukt de capaciteit van de condensator om lading vast te houden, wat direct invloed heeft op de spanning die het vertoont.Tijdens de werking is de dynamiek van het opladen en ontladen van de condensator van vitaal belang voor het begrijpen van RC -circuits.De tijdconstante (τ), gedefinieerd als  , meet hoe snel de condensator ongeveer 63,2% van de volledige spanning bereikt die door de bron wordt geleverd (V0).Deze tijdconstante is een indicatie van hoe het circuit zich aanpast aan het invoeren van veranderingen, waarbij de weerstand- en condensator -eigenschappen het tempo van deze aanpassingen dicteren.
, meet hoe snel de condensator ongeveer 63,2% van de volledige spanning bereikt die door de bron wordt geleverd (V0).Deze tijdconstante is een indicatie van hoe het circuit zich aanpast aan het invoeren van veranderingen, waarbij de weerstand- en condensator -eigenschappen het tempo van deze aanpassingen dicteren.
 .Deze relatie benadrukt de capaciteit van de condensator om lading vast te houden, wat direct invloed heeft op de spanning die het vertoont.Tijdens de werking is de dynamiek van het opladen en ontladen van de condensator van vitaal belang voor het begrijpen van RC -circuits.De tijdconstante (τ), gedefinieerd als
.Deze relatie benadrukt de capaciteit van de condensator om lading vast te houden, wat direct invloed heeft op de spanning die het vertoont.Tijdens de werking is de dynamiek van het opladen en ontladen van de condensator van vitaal belang voor het begrijpen van RC -circuits.De tijdconstante (τ), gedefinieerd als  , meet hoe snel de condensator ongeveer 63,2% van de volledige spanning bereikt die door de bron wordt geleverd (V0).Deze tijdconstante is een indicatie van hoe het circuit zich aanpast aan het invoeren van veranderingen, waarbij de weerstand- en condensator -eigenschappen het tempo van deze aanpassingen dicteren.
, meet hoe snel de condensator ongeveer 63,2% van de volledige spanning bereikt die door de bron wordt geleverd (V0).Deze tijdconstante is een indicatie van hoe het circuit zich aanpast aan het invoeren van veranderingen, waarbij de weerstand- en condensator -eigenschappen het tempo van deze aanpassingen dicteren.De spanning over de condensator op een bepaald moment tijdens de lading wordt gegeven door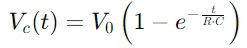 , het illustreren van een niet-lineaire toename terwijl de condensator vult.Deze vergelijking beschrijft hoe de ladingssnelheid vertraagt naarmate de condensator de volledige capaciteit nadert.
, het illustreren van een niet-lineaire toename terwijl de condensator vult.Deze vergelijking beschrijft hoe de ladingssnelheid vertraagt naarmate de condensator de volledige capaciteit nadert.
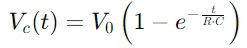 , het illustreren van een niet-lineaire toename terwijl de condensator vult.Deze vergelijking beschrijft hoe de ladingssnelheid vertraagt naarmate de condensator de volledige capaciteit nadert.
, het illustreren van een niet-lineaire toename terwijl de condensator vult.Deze vergelijking beschrijft hoe de ladingssnelheid vertraagt naarmate de condensator de volledige capaciteit nadert.Omgekeerd daalt de spanning van de condensator tijdens ontslag volgens de spanning  , het weergeven van een lineaire afname van opgeslagen energie in de loop van de tijd.Dit proces geeft een duidelijk beeld van hoe energie wordt vrijgegeven uit de condensator terug in het circuit.In AC -toepassingen is het faseverschil tussen de spanning en stroom, φ, wordt kritisch.Dit verschil, berekend als
, het weergeven van een lineaire afname van opgeslagen energie in de loop van de tijd.Dit proces geeft een duidelijk beeld van hoe energie wordt vrijgegeven uit de condensator terug in het circuit.In AC -toepassingen is het faseverschil tussen de spanning en stroom, φ, wordt kritisch.Dit verschil, berekend als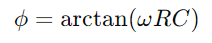 waar Ω vertegenwoordigt hoekfrequentie, toont de vertraging veroorzaakt door de condensator, die de timing beïnvloedt tussen wanneer stroomstromen en spanningsveranderingen over de componenten.
waar Ω vertegenwoordigt hoekfrequentie, toont de vertraging veroorzaakt door de condensator, die de timing beïnvloedt tussen wanneer stroomstromen en spanningsveranderingen over de componenten.
 , het weergeven van een lineaire afname van opgeslagen energie in de loop van de tijd.Dit proces geeft een duidelijk beeld van hoe energie wordt vrijgegeven uit de condensator terug in het circuit.In AC -toepassingen is het faseverschil tussen de spanning en stroom, φ, wordt kritisch.Dit verschil, berekend als
, het weergeven van een lineaire afname van opgeslagen energie in de loop van de tijd.Dit proces geeft een duidelijk beeld van hoe energie wordt vrijgegeven uit de condensator terug in het circuit.In AC -toepassingen is het faseverschil tussen de spanning en stroom, φ, wordt kritisch.Dit verschil, berekend als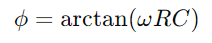 waar Ω vertegenwoordigt hoekfrequentie, toont de vertraging veroorzaakt door de condensator, die de timing beïnvloedt tussen wanneer stroomstromen en spanningsveranderingen over de componenten.
waar Ω vertegenwoordigt hoekfrequentie, toont de vertraging veroorzaakt door de condensator, die de timing beïnvloedt tussen wanneer stroomstromen en spanningsveranderingen over de componenten.Over het algemeen beperkt en stuurt de weerstand de stroomstroom terwijl de condensator de spanning opslaat en moduleert.Samen bepalen ze de responskenmerken van het circuit, zoals hoe snel het kan laden en ontladen en de faseverschuivingen die optreden in wisselstroomscenario's.Dit gecombineerde gedrag ondersteunt de fundamentele activiteiten van RC -seriecircuits, waardoor ze integraal zijn in verschillende elektronische toepassingen.
Basisvergelijkingen van RC Series Circuit
Om het gedrag van een RC -seriecircuit te begrijpen, is het cruciaal om te beginnen met de basisvergelijkingen die de reactie op veranderingen in de ingangsspanning beschrijven.Ga ervan uit dat we een veranderende ingangsspanning hebben weergegeven als Vin (t), met de spanning over de weerstand gelabeld als VR (T) en over de condensator als VC (T).In een seriecircuit, dezelfde stroom, Het) stroomt door zowel de weerstand als de condensator.
Het toepassen van de spanningswet van Kirchhoff (KVL), waarin staat dat de totale spanning rond elke gesloten lus in een circuit gelijk moet zijn, vinden we dat de ingangsspanning gelijk is aan de som van de spanningen over de weerstand en de condensator:
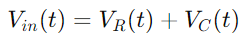
De spanning over de weerstand kan worden berekend met behulp van de wet van Ohm:
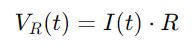
Voor de condensator is de spanning VC (t) gerelateerd aan de lading q (t) die het vasthoudt, gegeven door:
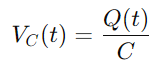
Omdat de stroom wordt gedefinieerd als de snelheid van ladingstroom, hebben we:
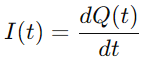
Door te vervangen Q (t) in de vergelijking voor VC (T), en het gebruik van de afgeleide van lading Het), we leiden de kerndifferentiaalvergelijking af voor het RC -seriecircuit:
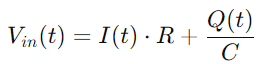
Verder vervangen Q (t) met de integraal van Het), we krijgen:
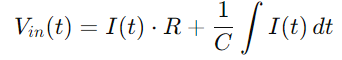
Voor de huidige I (t), gezien de snelheid van spanningssnelheid over de condensator, gebruiken we:
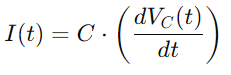
Het integreren van al deze relaties geeft ons de differentiaalvergelijking die de spanning over de condensator beschrijft:
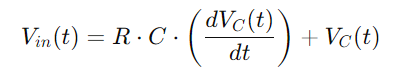
Dit is een lineaire differentiaalvergelijking van de eerste orde die de tijdsafhankelijke spanningsverandering over de condensator vastlegt.Door deze vergelijking op te lossen, kunnen we precies beschrijven hoe de condensatorspanning evolueert.Dit begrip is fundamenteel voor het analyseren van zowel de laad- als het ontladen van cycli van de condensator, evenals de reactie van het circuit op verschillende frequenties.Deze uitgebreide aanpak biedt een diep inzicht in de dynamische kenmerken van het RC -seriecircuit.
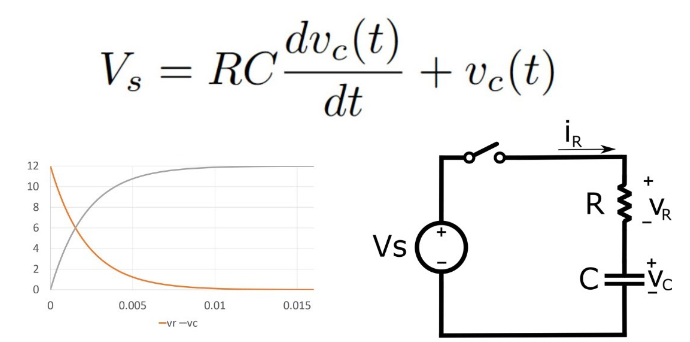
Figuur 6: Spanningsdifferentiaalvergelijking
Impedantie van RC Series Circuit
Om de beschrijving van een RC-seriecircuit te herschrijven, met een focus op menselijke interactie en een directe, vereenvoudigde uitleg, laten we de tastbare ervaringen en stapsgewijze bewerkingen verbeteren met behoud van de kernboodschap en coherentie:
In een RC -seriecircuit werken de weerstand en de condensator samen om de stroom van elektriciteit te regelen, cruciaal bij het omgaan met afwisselende stromingen.De totale impedantie van het circuit, weergegeven als 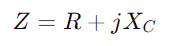 , combineert de weerstand R en de capacitieve reactantie XC.Het belangrijkste kenmerk van deze opstelling is dat de impedantiewaarden voor beide componenten variëren met frequentieveranderingen.Naarmate de frequentie toeneemt, neemt de impedantie van de condensator af, waardoor er meer stroom door kan gaan, terwijl de weerstand in wezen constant blijft.
, combineert de weerstand R en de capacitieve reactantie XC.Het belangrijkste kenmerk van deze opstelling is dat de impedantiewaarden voor beide componenten variëren met frequentieveranderingen.Naarmate de frequentie toeneemt, neemt de impedantie van de condensator af, waardoor er meer stroom door kan gaan, terwijl de weerstand in wezen constant blijft.
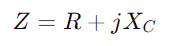 , combineert de weerstand R en de capacitieve reactantie XC.Het belangrijkste kenmerk van deze opstelling is dat de impedantiewaarden voor beide componenten variëren met frequentieveranderingen.Naarmate de frequentie toeneemt, neemt de impedantie van de condensator af, waardoor er meer stroom door kan gaan, terwijl de weerstand in wezen constant blijft.
, combineert de weerstand R en de capacitieve reactantie XC.Het belangrijkste kenmerk van deze opstelling is dat de impedantiewaarden voor beide componenten variëren met frequentieveranderingen.Naarmate de frequentie toeneemt, neemt de impedantie van de condensator af, waardoor er meer stroom door kan gaan, terwijl de weerstand in wezen constant blijft.De impedantie, aangeduid als Z en gemeten in ohm (ω), speelt een cruciale rol bij het bepalen van hoe het circuit reageert op een wisselstroom.Zoals in RL -serie circuits, de weerstand R en capacitieve reactantie xC van een RC -circuit vormt een driehoek bekend als de impedantiediange.Deze driehoek heeft nauw verband met de spanningsdriehoek en door de Pythagorese stelling toe te passen, kunt u de totale impedantie van het circuit berekenen.
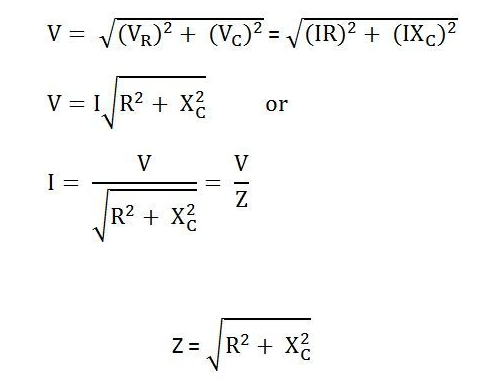
Afbeelding 7: RC -serie Circuit berekeningsformule
Overweeg een koptelefoons die deze principes gebruiken als het gaat om praktische toepassingen.High-impedantie hoofdtelefoons, vaak meer dan 200 ohm, worden meestal gebruikt met desktopcomputers, stroomversterkers en professionele audioapparatuur.Deze modellen met hoge impedantie komen goed overeen met de uitvoermogelijkheden van professionele elektronica.Wanneer u deze hoofdtelefoon gebruikt, is het cruciaal om het volume geleidelijk aan te passen om overbelasting te voorkomen en de delicate interne componenten, zoals de spraakspoel te beschadigen.
Omgekeerd hebben low-impedantie hoofdtelefoon, meestal lager dan 50 ohm, de voorkeur voor draagbare apparaten zoals CD-spelers, MD-spelers of MP3-spelers.Deze hoofdtelefoons vereisen minder vermogen om audio van hoge kwaliteit te leveren, waardoor ze ideaal zijn voor mobiel gebruik.Ze vereisen echter ook zorgvuldige aandacht voor gevoeligheidsniveaus om optimale prestaties te garanderen en schade aan de koptelefoon of gehoor te voorkomen.
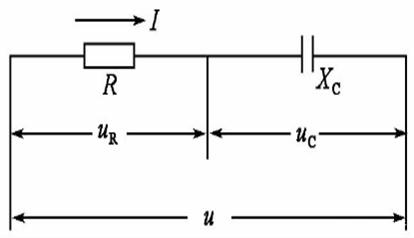
Figuur 8: Impedantiediagram van RC -serie circuit
Toegangs- en analyseprocedures van RC -serie circuits
Toegangsmaatregelen meet hoe gemakkelijk een RC -seriecircuit elektriciteit kan leiden, berekend als het omgekeerde van impedantie (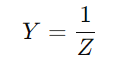 ).Deze waarde integreert zowel de weerstand (R) en de reactantie (X) van het circuit.Weerstand verzet zich tegen de stroomstroom door elektrische energie om te zetten in warmte, terwijl reactantie energie tijdelijk in het circuit opslaat.
).Deze waarde integreert zowel de weerstand (R) en de reactantie (X) van het circuit.Weerstand verzet zich tegen de stroomstroom door elektrische energie om te zetten in warmte, terwijl reactantie energie tijdelijk in het circuit opslaat.
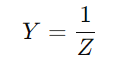 ).Deze waarde integreert zowel de weerstand (R) en de reactantie (X) van het circuit.Weerstand verzet zich tegen de stroomstroom door elektrische energie om te zetten in warmte, terwijl reactantie energie tijdelijk in het circuit opslaat.
).Deze waarde integreert zowel de weerstand (R) en de reactantie (X) van het circuit.Weerstand verzet zich tegen de stroomstroom door elektrische energie om te zetten in warmte, terwijl reactantie energie tijdelijk in het circuit opslaat.Om toegang te berekenen
Begin met het schrijven van de impedantie 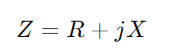 , waar r staat voor weerstand, X voor reactantie, en J is de denkbeeldige eenheid.Gebruik de formule y = 1/(R + jx).Deze bewerking omvat complexe nummers en geeft ons
, waar r staat voor weerstand, X voor reactantie, en J is de denkbeeldige eenheid.Gebruik de formule y = 1/(R + jx).Deze bewerking omvat complexe nummers en geeft ons  .Hier, G is de geleiding (werkelijke stroomstroomcapaciteit) en B is de gevoeligheid (het vermogen van het circuit om te reageren op veranderingen in stroom).
.Hier, G is de geleiding (werkelijke stroomstroomcapaciteit) en B is de gevoeligheid (het vermogen van het circuit om te reageren op veranderingen in stroom).
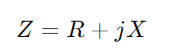 , waar r staat voor weerstand, X voor reactantie, en J is de denkbeeldige eenheid.Gebruik de formule y = 1/(R + jx).Deze bewerking omvat complexe nummers en geeft ons
, waar r staat voor weerstand, X voor reactantie, en J is de denkbeeldige eenheid.Gebruik de formule y = 1/(R + jx).Deze bewerking omvat complexe nummers en geeft ons  .Hier, G is de geleiding (werkelijke stroomstroomcapaciteit) en B is de gevoeligheid (het vermogen van het circuit om te reageren op veranderingen in stroom).
.Hier, G is de geleiding (werkelijke stroomstroomcapaciteit) en B is de gevoeligheid (het vermogen van het circuit om te reageren op veranderingen in stroom).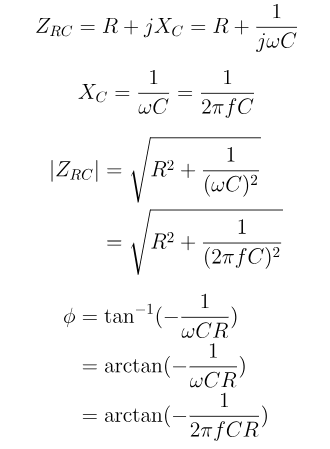
Figuur 9: Serie RC Circuit Impedance Calculator
Deze berekening onthult niet alleen de geleidbaarheid van het circuit, maar ook de dynamische responskenmerken, cruciaal voor AC -circuitanalyse.Geleiding en gevoel, samen genomen, geven aan hoe het circuit stroom passeert en hoe het opslaat en energie vrijgeeft.
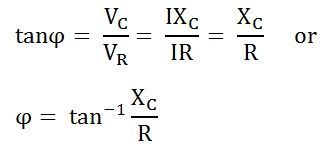
Figuur 10: Fasehoekformule
Praktische toepassing
Ingenieurs gebruiken toegangswaarden om het circuitontwerp te verbeteren, vooral in hoogfrequente toepassingen zoals radiofrequentiecircuits.Het aanpassen van toegang helpt bij het matchen van impedantie, het verminderen van signaalreflectie en het stimuleren van de transmissie -efficiëntie.
Door de toelatingsrespons te bestuderen, kunnen ingenieurs circuitprestaties beoordelen en voorspellen onder verschillende omstandigheden, zoals frequentierespons, stabiliteit en gevoeligheid.Uitrusten met een oscilloscoop en een signaalgenerator om de spanning en stroom van het circuit te meten bij verschillende frequenties.Focus vooral op de afsnijfrequentie om theoretische voorspellingen te testen en te valideren tegen praktische observaties.Begin voor AC -circuits met het bepalen van de reactantie (XC) van de condensator met 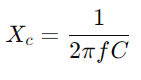 , waar F is de signaalfrequentie.Bereken de totale impedantie
, waar F is de signaalfrequentie.Bereken de totale impedantie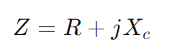 En dan toelating
En dan toelating 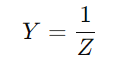 .
.
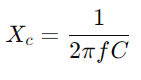 , waar F is de signaalfrequentie.Bereken de totale impedantie
, waar F is de signaalfrequentie.Bereken de totale impedantie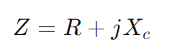 En dan toelating
En dan toelating 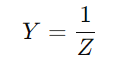 .
.Analyseer faseverschil met behulp van  om de signaalvormwijziging te begrijpen.Onderzoek hoe het circuit met verschillende frequenties omgaat, met name het gedrag op de afsnijdfrequentie opmerken
om de signaalvormwijziging te begrijpen.Onderzoek hoe het circuit met verschillende frequenties omgaat, met name het gedrag op de afsnijdfrequentie opmerken 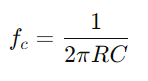 , waar het circuit verschuift van passeren naar bloksignalen.Het evalueren van hoe impedantie en faseverschil variëren met frequentie, is cruciaal voor het ontwerpen van effectieve filters en signaalprocessors.Bespreek hoe frequentieselectiviteit, faseverschuivingen en signaalverzwakking als gevolg van de eigenschappen van het circuit van invloed zijn op praktische toepassingen zoals filteren en elektronische afstemming.
, waar het circuit verschuift van passeren naar bloksignalen.Het evalueren van hoe impedantie en faseverschil variëren met frequentie, is cruciaal voor het ontwerpen van effectieve filters en signaalprocessors.Bespreek hoe frequentieselectiviteit, faseverschuivingen en signaalverzwakking als gevolg van de eigenschappen van het circuit van invloed zijn op praktische toepassingen zoals filteren en elektronische afstemming.
 om de signaalvormwijziging te begrijpen.Onderzoek hoe het circuit met verschillende frequenties omgaat, met name het gedrag op de afsnijdfrequentie opmerken
om de signaalvormwijziging te begrijpen.Onderzoek hoe het circuit met verschillende frequenties omgaat, met name het gedrag op de afsnijdfrequentie opmerken 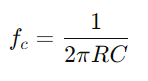 , waar het circuit verschuift van passeren naar bloksignalen.Het evalueren van hoe impedantie en faseverschil variëren met frequentie, is cruciaal voor het ontwerpen van effectieve filters en signaalprocessors.Bespreek hoe frequentieselectiviteit, faseverschuivingen en signaalverzwakking als gevolg van de eigenschappen van het circuit van invloed zijn op praktische toepassingen zoals filteren en elektronische afstemming.
, waar het circuit verschuift van passeren naar bloksignalen.Het evalueren van hoe impedantie en faseverschil variëren met frequentie, is cruciaal voor het ontwerpen van effectieve filters en signaalprocessors.Bespreek hoe frequentieselectiviteit, faseverschuivingen en signaalverzwakking als gevolg van de eigenschappen van het circuit van invloed zijn op praktische toepassingen zoals filteren en elektronische afstemming.Deze aanpak splitst de operationele processen af in beheersbare stappen, waardoor het begrip van de gebruiker wordt verrijkt met praktische inzichten in het hanteren en analyseren van RC -seriecircuits.
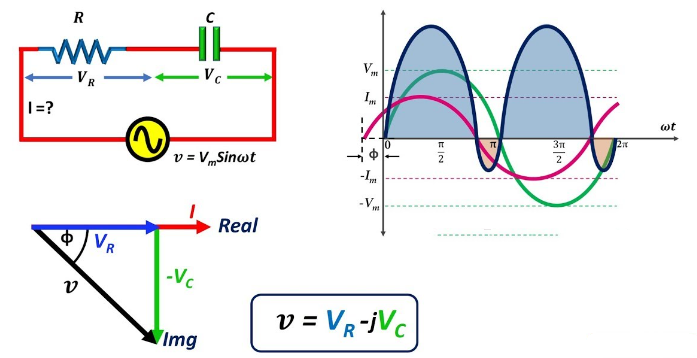
Figuur 11: Kenmerken van Circuits van RC -serie
Phasor Diagram van RC Series Circuit
In een RC -seriecircuit delen alle elementen dezelfde stroom vanwege hun serieconfiguratie.Deze uniforme stroom fungeert als een basislijn voor ons phasor -diagram, dat helpt bij het visualiseren van de relatie tussen verschillende spanningen en stromen in het circuit.Laten we deze stroom aanwijzen I als referentie phasor, geplaatst op nul graden op het diagram.In het diagram, de stroom I wordt horizontaal aan de rechterkant ingesteld en wordt de nul-graads referentielijn vastgesteld.De spanning over de weerstand (UR) is in fase met de stroom omdat weerstanden geen faseverschuiving veroorzaken.Dus, UR wordt getekend als een horizontale vector in dezelfde richting als I, zich uitstrekkend van de oorsprong.
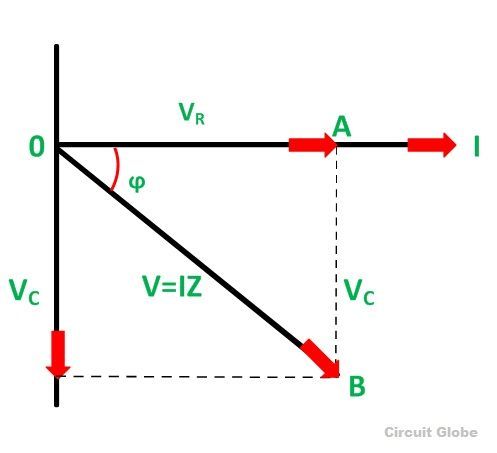
Figuur 12: RC -serie Circuit Phasor Diagram
Daarentegen de spanning over de condensator (UC) leidt de stroom met 90 graden vanwege de capacitieve eigenschap van het uitstellen van de huidige fase.Deze spanning wordt weergegeven door een verticale vector die naar boven wijst, beginnend bij de punt van de UR vector.De totale spanning U In het circuit staat de vectorgom van U Rand UC.Deze som vormt een juiste driehoek met UR En UC als de aangrenzende en tegenovergestelde zijden, respectievelijk.De hypotenusa van deze driehoek, die zich uitstrekt van de oorsprong tot de punt van de UC vector, vertegenwoordigt U.
De sinusvormige stroom door het circuit wordt gegeven door zonde (ωt), waarbij IM de maximale stroomamplitude is en Ω is de hoekfrequentie.Bijgevolg is de spanning over de weerstand 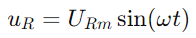 , spiegelt de huidige golfvorm.De spanning over de condensator wordt gegeven door
, spiegelt de huidige golfvorm.De spanning over de condensator wordt gegeven door 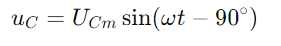 , wat een faseverschuiving van -90 ° (of 90 graden voor de stroom) aangeeft.De rechter driehoek van het phasor -diagram verduidelijkt dat
, wat een faseverschuiving van -90 ° (of 90 graden voor de stroom) aangeeft.De rechter driehoek van het phasor -diagram verduidelijkt dat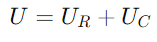 is niet alleen in grootte, maar ook in de faserelatie, met de terminale spanningsvector (U) het voltooien van de driehoek.
is niet alleen in grootte, maar ook in de faserelatie, met de terminale spanningsvector (U) het voltooien van de driehoek.
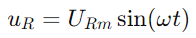 , spiegelt de huidige golfvorm.De spanning over de condensator wordt gegeven door
, spiegelt de huidige golfvorm.De spanning over de condensator wordt gegeven door 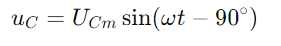 , wat een faseverschuiving van -90 ° (of 90 graden voor de stroom) aangeeft.De rechter driehoek van het phasor -diagram verduidelijkt dat
, wat een faseverschuiving van -90 ° (of 90 graden voor de stroom) aangeeft.De rechter driehoek van het phasor -diagram verduidelijkt dat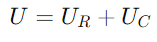 is niet alleen in grootte, maar ook in de faserelatie, met de terminale spanningsvector (U) het voltooien van de driehoek.
is niet alleen in grootte, maar ook in de faserelatie, met de terminale spanningsvector (U) het voltooien van de driehoek.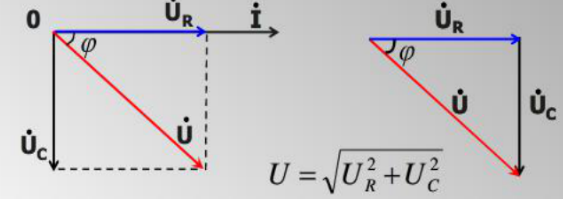
Afbeelding 13: Spanningsfasordiagram van RC Series Circuit
Belangrijke punten bij het analyseren van Series RC -circuits
Impedantie in serie RC -circuit, weergegeven als Z, combineert weerstand (R) en het reactieve effect van capaciteit in een enkele maat die varieert met signaalfrequentie.Het wordt wiskundig uitgedrukt als 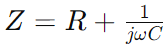 , waar Ω is de hoekfrequentie en C is de capaciteit.Hier, R vormt het werkelijke deel van de impedantie, en
, waar Ω is de hoekfrequentie en C is de capaciteit.Hier, R vormt het werkelijke deel van de impedantie, en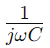 vertegenwoordigt het denkbeeldige deel, dat aangeeft hoe de condensator het circuit beïnvloedt.
vertegenwoordigt het denkbeeldige deel, dat aangeeft hoe de condensator het circuit beïnvloedt.
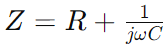 , waar Ω is de hoekfrequentie en C is de capaciteit.Hier, R vormt het werkelijke deel van de impedantie, en
, waar Ω is de hoekfrequentie en C is de capaciteit.Hier, R vormt het werkelijke deel van de impedantie, en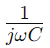 vertegenwoordigt het denkbeeldige deel, dat aangeeft hoe de condensator het circuit beïnvloedt.
vertegenwoordigt het denkbeeldige deel, dat aangeeft hoe de condensator het circuit beïnvloedt.De manier waarop impedantie verandert met frequentie is cruciaal voor het gebruik van serie RC -circuits in filtertoepassingen.Bij lagere frequenties vertoont het circuit hogere impedantie, waardoor deze frequenties effectief worden geblokkeerd.Omgekeerd, bij hogere frequenties, daalt de impedantie, waardoor deze frequenties vrijer kunnen passeren.Dit gedrag maakt serie RC-circuits ideaal voor taken zoals het filteren van ongewenste laagfrequente ruis of het passeren van hoogfrequente signalen.

Figuur 14: Impedantie vectordiagram van RC -serie circuit
Conclusie
Van het filteren van ongewenste frequenties tot het vormgeven van signaalreacties, het RC -seriecircuit is een belangrijke rol in een breed scala van elektronische functies.Door de onderliggende principes zoals impedantie, fasorrelaties en het frequentie-afhankelijke gedrag van deze circuits, zijn ingenieurs en ontwerpers uitgerust met ambachtelijke oplossingen die de signaalintegriteit in complexe elektronische systemen effectief beheren.Het gedetailleerde onderzoek van deze circuits, ondersteund door wiskundige analyse en visuele representaties zoals fasordiagrammen, biedt een uitgebreid inzicht dat belangrijk is voor iedereen die hun begrip van elektronische circuitdynamiek wil verdiepen of hun praktische vaardigheden in circuitontwerp en probleemoplossing wil verbeteren.
Veelgestelde vragen [FAQ]
1. Wat is het principe van RC Circuit?
Het principe van een RC-circuit (weerstandsbandidaat) draait om de laad- en ontlaadprocessen van de condensator door de weerstand.In dit circuit interageert het vermogen van de condensator om elektrische energie op te slaan en vrij te geven met de weerstand, die de snelheid regelt waarmee de condensator laadt of ontladen.
2. Waarom leidt een RC -circuit de stroomstroom?
In een RC -circuit leidt de stroom de spanning over de condensator omdat de condensator moet beginnen met opladen voordat de spanning kan stijgen.Omdat de stroom in de condensator stroomt om deze op te laden, piekt de stroom voordat de spanning over de condensator zijn maximum bereikt.Dit effect veroorzaakt een faseverschuiving waarbij de stroomfase de spanningsfase met maximaal 90 graden leidt, afhankelijk van de frequentie van het ingangssignaal.
3. Hoe verandert spanning in een RC -circuit?
De spanningsverandering in een RC -circuit tijdens het opladen wordt beschreven door een exponentiële functie.Wanneer een spanning wordt toegepast, neemt de spanning over de condensator aanvankelijk snel toe en vertraagt dan naarmate deze de voedingsspanning nadert.Wiskundig wordt dit uitgedrukt als 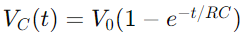 , waar VC(T) is de spanning over de condensator op tijdstip t, v0 is de voedingsspanning en RC is de tijdconstante van het circuit, waarbij wordt bepaald hoe snel de condensator oplaadt.Omgekeerd neemt de spanning over de condensator tijdens het afladen exponentieel af, na de vergelijking
, waar VC(T) is de spanning over de condensator op tijdstip t, v0 is de voedingsspanning en RC is de tijdconstante van het circuit, waarbij wordt bepaald hoe snel de condensator oplaadt.Omgekeerd neemt de spanning over de condensator tijdens het afladen exponentieel af, na de vergelijking 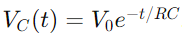 .
.
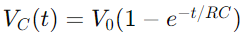 , waar VC(T) is de spanning over de condensator op tijdstip t, v0 is de voedingsspanning en RC is de tijdconstante van het circuit, waarbij wordt bepaald hoe snel de condensator oplaadt.Omgekeerd neemt de spanning over de condensator tijdens het afladen exponentieel af, na de vergelijking
, waar VC(T) is de spanning over de condensator op tijdstip t, v0 is de voedingsspanning en RC is de tijdconstante van het circuit, waarbij wordt bepaald hoe snel de condensator oplaadt.Omgekeerd neemt de spanning over de condensator tijdens het afladen exponentieel af, na de vergelijking 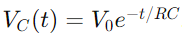 .
. OVER ONS
Klanttevredenheid elke keer.Wederzijds vertrouwen en gemeenschappelijke belangen.
OVER ONS
Klanttevredenheid elke keer.Wederzijds vertrouwen en gemeenschappelijke belangen.
Functietest.De hoogste kosteneffectieve producten en de beste service zijn onze eeuwige inzet.
Heet artikel
- Zijn CR2032 en CR2016 uitwisselbaar
- MOSFET: Definitie, werkingsprincipe en selectie
- Relaisinstallatie en testen, interpretatie van relaisbedradingsdiagrammen
- CR2016 vs. CR2032 Wat is het verschil
- NPN vs. PNP: Wat is het verschil?
- ESP32 vs STM32: Welke microcontroller is beter voor u?
- LM358 Dubbele operationele versterker uitgebreide gids: pinouts, circuitdiagrammen, equivalenten, nuttige voorbeelden
- CR2032 vs DL2032 vs CR2025 Vergelijkingsgids
- Inzicht in de verschillen ESP32 en ESP32-S3 Technische en prestatie-analyse
- Gedetailleerde analyse van RC Series Circuit
 Diepgaande analyse van 1N4148-diodes: bedrijfsmodi, specificaties en gebruiksscenario's
Diepgaande analyse van 1N4148-diodes: bedrijfsmodi, specificaties en gebruiksscenario's
2024-05-08
 Inzicht in de typen en gebruik van dynamische en positieve verplaatsingspompen
Inzicht in de typen en gebruik van dynamische en positieve verplaatsingspompen
2024-05-07
Heet onderdeelnummer
 C2012CH2W392K125AA
C2012CH2W392K125AA C0402C0G1C470J020BC
C0402C0G1C470J020BC C0402C0G1C4R3B
C0402C0G1C4R3B C1005X8R1H151M050BE
C1005X8R1H151M050BE M39003/01-6024
M39003/01-6024 AK4497EQ
AK4497EQ AT49F001AN-55JU
AT49F001AN-55JU VE-J50-IY
VE-J50-IY VE-202-IX
VE-202-IX RT0402DRD07100RL
RT0402DRD07100RL
- ATF22V10CQZ-20XU
- AT28HC256-90PC
- AT27BV010-90VC
- AP7365-18EG-13
- 1MBI900VXA-120PD-50
- CM150TF-12E
- UCC2809PTR-2G4
- LT1791AIS#PBF
- PAM8904JPR
- MC33179DR2
- CD74AC151M96
- T491D476K016AT24787027
- A42MX16PL84-1
- BSC050N04NS3G
- CMR2-04TR13
- CY2292SC-492T
- INA322EA/2K5G4
- K4M28163LF-RS75
- M27W064-100M1
- MB89653ARPFV-G-364-BND
- MBM29F400TC-70PFTN-SFE
- MC3372DR2
- MSM514400D-60TS-K
- PC123ZY1J100F
- PPC750L-GB400A2
- R5F2135CMNFP
- TMP87PM78F
- TMS470CS241C023PNT
- USX2014-NU-04
- X9261TV24IZ-2.7
- C1210X472KGRACTU
- 4N60L
- CT675B-LF
- HD64F2646RFC20JV
- INA253A2QPWRQ1
- IDRD51-0-A1F1C-32C
- CYAT81688-128AS88Z
- 2000-1492
- AP64060WU-7